RAID5, URE and the probability

So you may have heard that RAID5 is doomed due to this “URE”.

What does it mean? Is it true? Let’s find out.

Note: we will talk about mechanical “hard” disks.

URE: Unrecoverable Read Error

URE, Unrecoverable read error, is an attribute of a disk. It represents the probability of a read error while reading a bit from the disk. In consumer-grade disks, this value is usually < 10^-14 (less than one bit per ~10TiB). Enterprise-grade disks are certified for 10^-15.

It doesn’t mean that you will have an error after ~10TiB. It means that, for each 10TiB, there is a non-negligible probability of encountering a read error. It may never happen, or it might happen.

When a read error occurs, the content of the sector is lost. If the filesystem is not aware or cannot restore the content, the filesystem itself (or a single file) can be damaged.

RAID

RAID, Redundant array of inexpensive disks, is a way to use disks to increase redundancy by having multiple copies (or parity blocks) across multiple disks. As a consequence of this, some RAID configurations might provide better performance in reading/writing.

RAID also comes with penalities: some configurations may have slower writes (e.g., in RAID1 we need to wait until the slowest disk finishes its write sequence), and nearly all levels require sacrificing some space.

For more details, the Wikipedia page on RAID is very well written.

RAID5

In short: in RAID5, each sequence of blocks (“stripe size”) terminates with a parity block. The parity block is used to rebuild the block of a failed disk. The usable size is the sum of raw disk sizes for all but one disk (because of the parity).

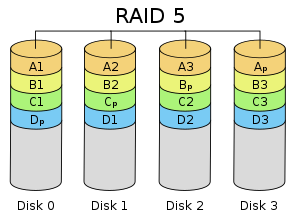
RAID5

(image courtesy of Wikipedia)

What happens when a disk fails? Let’s assume that the leftmost disk is out. When you replace it, the RAID controller will read A2, A3 and Ap (parity block), and it can re-calculate A1.

So, what is the problem here with RAID5?

For simplicity, let’s assume that we’re talking about RAID5. This problem applies even to other RAID levels in different ways.

When a disk in a RAID5 array fails, the array goes into a degraded state. In this state, it continues to serve requests from the operating system, but it won’t survive other failures.

To recover from a degraded state, the array needs to resilver or rebuild. This process will read the data from active (healthy) disks and “generates” the data for the replacement disk (the disk that was sitting as hot-spare or the new disk that the sysadmin installed in place of the defective one).

When you read everything from the array, the amount of data you need to read can be huge. Remember the URE? It turns out that, even if URE probability is very low (“less than one bit in ~10TiB”), when you apply this number to current disk sizes, the result can be significant. In math, we need to elevate the probability of success reading one bit (1 - URE_probability) to the number of bits that we will read:

probability_of_success = (1 - URE_probability)^((n_disks - 1) * total_bits_in_array)

Where:

When a URE happens during the resilver/rebuild process, the nightmare: the rebuild is stopped, and the RAID crashes. In practice, some controllers re-tries to read the sector, hoping that the URE was a software error and not a disk surface anomaly.

To make things clear, let’s make an example with numbers: let’s assume that we have an array of 4 disks (all in use) in RAID5, and each disk has a capacity of 6TiB. For simplicity, let’s assume that the array is full. The formula will be:

probability_of_success = (1 - 10^-14)^((4 - 1) * 6 * 8 * 10^12)

Where 6 * 8 * 10^12 is 6TiB. If you run the math, you will have 0.23720061006598592, which means that, on average, you’ll have 23.72% probability of success. In other words, when one disk fails, you may have one chance over four to rebuild the array without error.

Wait! You just used “may”. Is the math incorrect?

No. However, this math assumes these things:

So, reality can be better, far better. Some people may have petabytes of data on RAID without any issue.

However, don’t be deceived by this: the fact that some people are lucky doesn’t mean that you will be too. Don’t push your luck.

Conclusion

RAID5 is doomed because of URE? Is URE dangerous? It depends on how much risk you want to have. There is no way to remove UREs from disks, but we can avoid multiplying that small probability with big numbers.

One way is to use RAID levels wisely. For example, 4 x 6TiB disks may form a RAID10 array with 12TiB free space. The probability of success will be much higher, as now the rebuild will need to read 6TiB only (99.9999999995% of success in the worst-case scenario) instead of 18TiB.

URE and RAID10

Note: this also applies to RAID6 vs. RAID10, with slightly different numbers.

RAID10 (aka RAID1+0) arrays are built using a stripe over RAID1 disks. When you have multiple disks and want to combine them, RAID10 is often used in place of RAID5. Both of them have some protections against faults while allowing the creation of big arrays.

In RAID10, we have a different architecture: disks are placed in a RAID1 “sets”. Usually, these sets are organized using RAID1 on two disks. Then, the entire set is joined in a RAID0 (striping) pool. The size of the RAID0 pool is the sum of RAID1 mirrors, which means (if we use two disks per RAID1 mirror) half of the sum of raw disks capacity.

RAID10

(image courtesy of Wikipedia)

Let’s see what happens when a disk fails. Assume that our leftmost disk is gone: when you replace the disk with a new one, the RAID controller will need to copy A1, A3, and other blocks from the other disk in the RAID1 mirror (2nd leftmost). Other disks are left untouched.

In practice, it’s like we’re dealing with one disk failure in a single RAID1 pool: the capacity that the controller will read (and write) is the size of the occupied by data in the RAID1, which (in this case) is the half of the overall RAID size. If your pool uses 6 disks instead of 4, that size is 1/3, and so on.

To make a numerical example (suppose 6TiB disks in a data-full RAID10, two disks per RAID1 set):

probability_of_success = (1 - 10^-14)^(6 * 8 * 10^12)

Note that we don’t have to deal with the number of disks in the pool: differently from RAID5, we can have 4 or 400 disks; the probability is the same. Your pool may be 100TiB (200 x 1TiB), and it’s the same probability as having 1TiB in RAID1 (2 x 1TiB).

Note that using RAID10 has one more advantage: the rebuilt time will be much less, as we don’t need to read data from ALL disks. Also, there is no latency on other disks in the pool, meaning that only one read/write request over two (when using 4 disks) or one over three (when using 6 disks) will be impacted by a slow read/write.

Bonus: debunking the debunk!

Someone on the web (and on Reddit) says that this whole problem doesn’t exist because it never happens in a test lab. If it never occurred to you, it might be because your disks are in good health, or you never noticed that. Or, it might be a case of survival bias.

It’s like saying that cats always land on their feet because you never saw a cat landing on its back.

Which obviously is not true.

Addendum: some nice plots about RAID and URE

Note that you need more disks with RAID10 to have the same pool size as RAID5. Here is a nice picture of the usable space based on the number of disks:

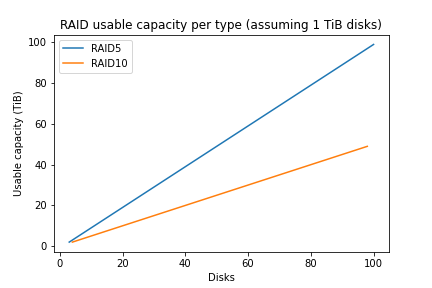
This is why people tend to use RAID5 (to maximize the usable space).

Also, by using the formula above, we can easily calculate the probability based on different factors. For example, we can see what happen if we have 1TiB disks and we want to build a big array (up to 50TiB):

Clearly, the probability for RAID10 is constant (the size of the disk is constant here), and it’s nearly 1 (meaning, always a success). RAID5 instead performs “good” only on small pools sizes.

See the same plot using 10TiB disks (note: the plot starts at 20TiB):

Here we can see that RAID10 is near 0.9, while RAID5 performs better than before (due to the smaller number of disks), but always well under RAID10.

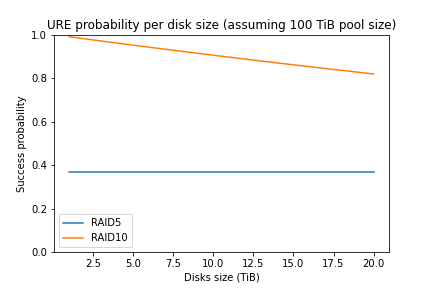
Finally, we can see how the probability changes based on the number of disks: in this case, we want a pool with 50TiB of usable size, and we want to know how the probability changes based on the size of disks (raw size, not usable size).

RAID5 has a constant probability because RAID5 needs to read the same amount of data each time: the whole pool size (50TiB). RAID10 instead performs better with smaller disks because the only part that it needs to read is one disk.

Increasing the pool size (e.g., to 100TiB) will negatively impact RAID5:

The notebook with some drafts is here: raid_calc.ipynb

#Sysadmin #RAID